Theoretical and Computational Biology is the latest addition to the diverse research areas of the School of Biology (SOB) at IISER Trivandrum, which aims at interdisciplinary research in biology by bringing biologists, physicists, and mathematicians together. My group is one of the first ones established under this mission. Through an interdisciplinary approach, we develop computational models to predict the outcome of a biological process, which guides new experiments to challenge the predictions and offers an optimized model-experiment framework for biological discoveries. We perform experiments to validate the predictions. The predictions made by the model and backed by experimental evidence help in discovering novel biological mechanisms.
Research
Regeneration of lost tissue and organs is significant during development. However, it is unclear how the lost organ regains its shape and how an organism knows which part of the organ to regenerate. In animals, cell migration near the cut site facilitates regeneration. Notably, cells are cemented in plants, and migration does not occur. Then the question is, what is the mechanism that facilitates the regeneration of lost tissue/organs in plants? The process of regeneration involves a complex coupling of cell geometry, mechanics, and biochemical signals. To understand this coupling, we develop computational models to simulate fundamental cellular behaviors such as microtubule self-organization and its impact on cell growth and division and make in-silico predictions. Further, using the developing root tip as a model system, we perform experiments to validate the predictions that help discover novel mechanisms of organ regeneration.
Please read more about the current research projects in our lab.

Fig 1: confocal display of endoderm-specific marker in Arabidopsis root
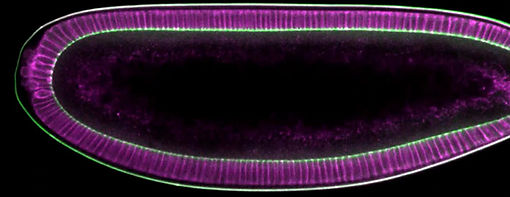
In animal morphogenesis during germband extension, the tissue undergoes a solid-fluid transition, which is driven by myosin planar polarity. The epithelial cells go through continuous changes in shape via active actomyosin remodeling, and this change in cell shape, in principle, should affect the associated cell polarity. This indicates there must be a mechanism that provides stability to the polarity cues against the changing cell shapes. Processes such as the efficiency of tissue repair or speed of cancer progression are also driven by the establishment of cell polarity, which needs to be stable even during changes in cell shapes, indicating the presence of feedback control. Uncovering these feedback mechanisms involves understanding the coupling of cell geometry with cell polarity. We develop computational models and perform experiments to understand the feedback control of cell polarity during dynamic tissue remodeling.
Please read more about the current research projects in our lab.